- Estimating Squares
- What A Derivative Is
- How To Calculate The Derivative
- Interlude: How To Visualize The Derivative
- Faq
- Power Rule, Chain Rule
- Recap
Contents
Introduction To Calculus With Derivatives

Suppose you need to calculate \(101^2\) but you don't have a calculator handy. How would you estimate it? \(100^2\) is pretty easy: \(100 * 100 = 10000\). But \(101^2\) seems tougher.

Or suppose you had to estimate \(4.1^2\). How would you do it? What about \(7.1^2\)? In all these cases, you know the square of a number that is pretty close (\(100^2\), \(4^2\), \(7^2\)). Can you use that to estimate this more difficult value?
What if I told you that \(4.1^2\) is \(16.81\). So that \(0.1\) change increased the square by \(0.81\) (from \(16\) to \(16.81\)). Does that mean \(7.1^2\) is \(49.81\) (because \(7^2\) is \(49\))? Or does it mean \(101^2\) is \(10008.1\) (\(100\) -> \(101\) is a change of \(1\), so just multiply the previous change of \(0.1\) by \(10\))?
Derivatives will help answer these questions. In this post, I'll first answer these questions using derivatives. Then I'll explain what a derivative is, and how to calculate it.
Estimating squares
\(4^2\) is \(16\), and \(4.1^2\) is \(16.81\). Adding that \(0.1\) to \(4\) increased the square by \(0.81\), i.e. an increase of ~\(8\) times (\(0.1 * 8 =~ 0.81\)).
\(5^2\) is \(25\), and \(5.1^2\) is \(26.01\). Adding that \(0.1\) to \(5\) increased the square by \(1.01\), i.e. an increase of ~\(10\) (\(0.1 * 10 =~ 1.01\)).
Lets look at some other increases:
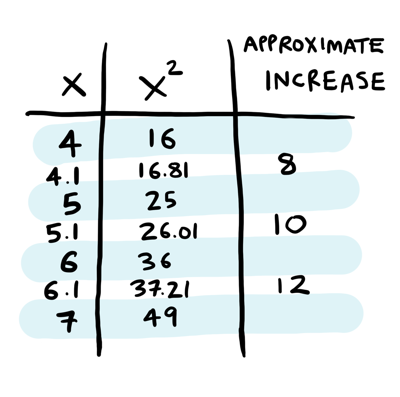
At \(4.1\), the increase was around \(8\). At \(5.1\), the increase was ~10. At \(6.1\), the increase was ~\(12\). Do you see the pattern? At \(7.1\), the increase must be around 14! All these numbers are roughly double the number we are trying to square (\(4.1\) -> \(8\), \(5.1\) -> \(10\), \(6.1\) -> \(12\), \(7.1\) -> \(14\)).
We know \(7^2\) is 49, and now we guess that there's an increase of 14 happening here. So to calculate \(7.1^2\), we need to increase that \(0.1\) by \(14\)! So \(7.1^2\) must be \(7^2 + 0.1*14\), or around \(50.4\):
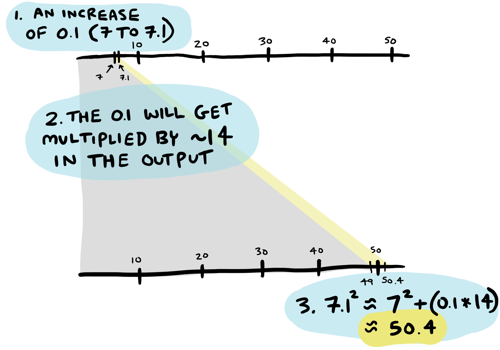
\(7.1^2\) is actually \(50.41\), so we were really close!
Going back to the original question, what is \(101^2\)? Well, there was an increase of \(1\) (from \(100\) to \(101\)). We know that will get multiplied by ~\(202\) in the square (\(101 * 2\)). So \(101^2\) must be \(100^2 + 202\), or around \(10202\). It is actually \(10201\), so again we were really close!
These numbers seem to magically tell you how to calculate values like \(4.1^2\), \(7.1^2\), or \(101^2\):
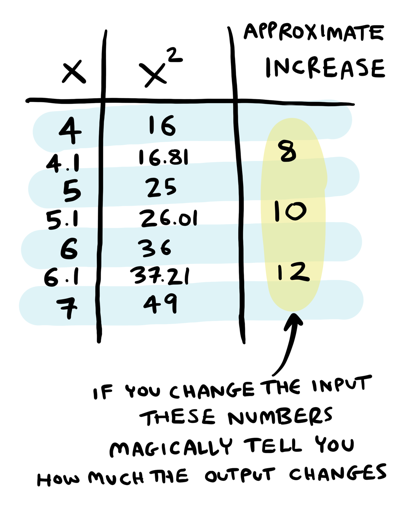
Here's the big reveal: those numbers are the derivative at those points. Let's make this a little more precise. We have been working with the square function \(f(x)\):
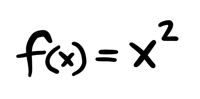
We know the value of \(f(x)\) for different values of \(x\):
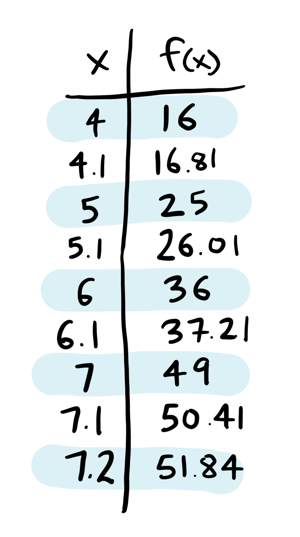
Here \(x\) is the input, and \(f(x)\) is the output. This whole time we have been changing the input (from \(4\) to \(4.1\) for example) and trying to guess the new output (i.e. if \(4^2 = 16\), what is \(4.1^2\)?)
The derivative of \(f(x)\) (written \(f'(x)\) -- note the apostrophe) is \(2x\). Here's the same table with a column for the derivative:

That last column has all the ratios we were just using! Notice the same pattern: the derivative at \(4\) is \(8\), at \(5\) it is \(10\) etc. Each time you just double the input to get the derivative.
Let's do another example and estimate \(5.1^2\). I know that \(5^2 = 25\), and the derivative at \(5\) is \(10\):
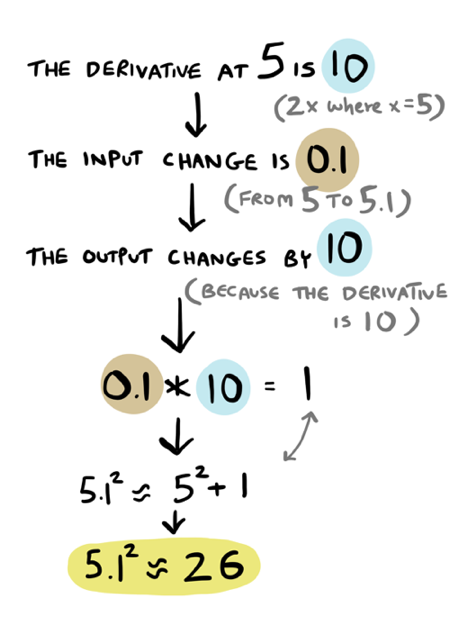
So our estimate is \(5.1^2 = 26\). The correct answer is \(26.01\), so we are again very close!
Let's recap some important things we learned:
- The derivative of the function \(f(x) = x^2\) is \(f'(x) = 2x\).
- This means, if we want to know \(101^2\) and we know the square of a close-by number like \(100^2\), we can figure out the change in input (\(1\)), multiply it by the derivative (\(202\)), and get the change in output (\(202\)). Then we know that \(101^2\) is approximately \(100^2\) plus \(202\).
Here is the most important takeaway from this whole blog post:

As you change the input, you can use the derivative to estimate how the output changes. Note: it is not an exact answer! It is merely a very good estimate.
What A Derivative Is
To recap, given some input change, the derivative tells us how the output will change. When we changed x from \(4\) to \(4.1\), the derivative told us that the output would change by a factor of \(8\).
This is the most important takeaway I had mentioned:

Written another way, a derivative is the ratio of output change to input change:
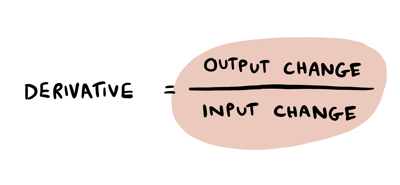
At \(4\), the derivative is \(8\). That means:
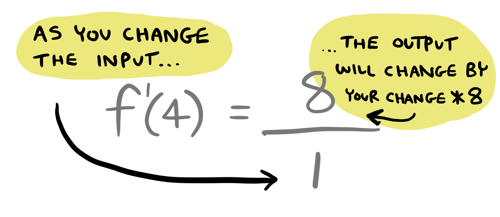
We can rearrange this fraction to get this:

This is how we have been using the derivative all along: multiplying the input change by the derivative to get the output change.
Earlier we had guessed the pattern that the output changes by around \(8\) at \(4.1\), around \(10\) at \(5.1\), around \(12\) at \(6.1\) etc. This was just our intuition, let's dig a little deeper.
How did we know that the output changed by around \(8\) at \(4.1\)? We did this math intuitively, in our heads:
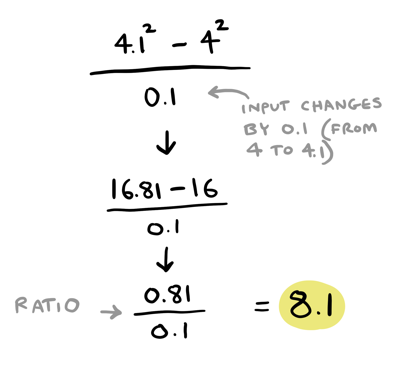
That looks suspiciously like a derivative!

With an input change of \(0.1\), the output change is \(0.81\). So the ratio is \(0.81/0.1\), or \(8.1\). We know the derivative at \(4\) is \(8\), and this is pretty close. It seems we basically calculated the derivative at \(4\)!
By the way, I've been using \(0.1\) as the input change because we were calculating \(4.1^2\) earlier. There's nothing special about \(0.1\) as the input change, it is just what I chose. You could choose other input changes:
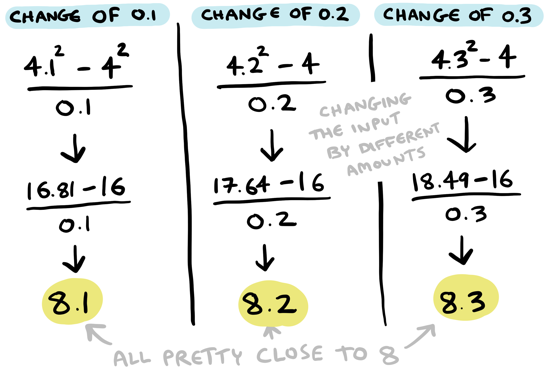
You can see that using \(0.1\), \(0.2\) or \(0.3\) as the input change, the ratios are all pretty close to \(8\). In all of these cases, we are pretty close to calculating the derivative at \(4\)! But here's something interesting -- the smaller the change, the closer the ratio is to \(8\):
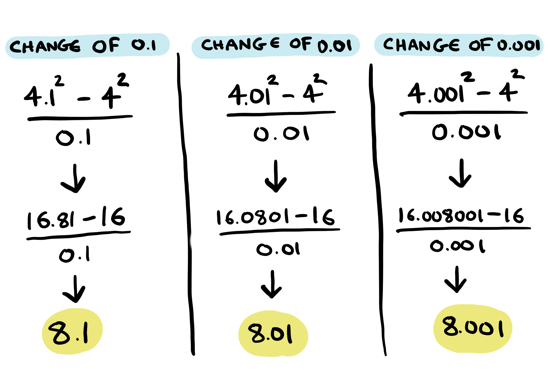
We will come back to this later on. For now, we will just say that since the ratio is getting closer and closer to \(8\) as we make the change smaller, the derivative at \(4\) is \(8\).
That was easy! By just calculating output change / input change, we figured out the derivative at \(4\) -- it's \(8\)! So if you ever need to figure out the derivative at a particular point, now you know how to do it.
Let's calculate the derivative at other numbers:
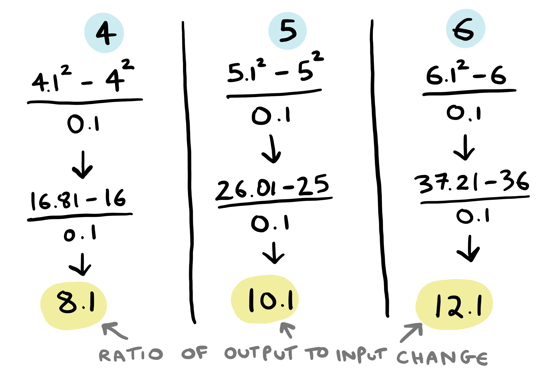
So the derivative at \(4\) is \(8\). At \(5\) it is \(10\), and at \(6\) it is \(12\). Remember earlier I had said the derivative of \(f(x) = x^2\) is \(f'(x) = 2x\)? This seems to match pretty well, doesn't it? To get the derivative at any number, you just double that number. Notice that even though the derivative is different at each number, the function stays the same: \(2x\):
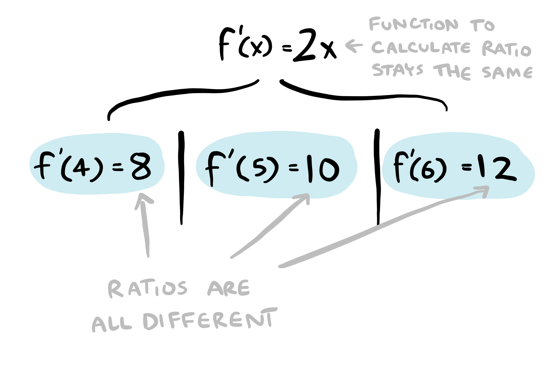
In this case, maybe we could have cleverly spotted this pattern ourselves. What about more complicated cases? For example, take the function \(f(x) = sqrt(x)\). What is its derivative?
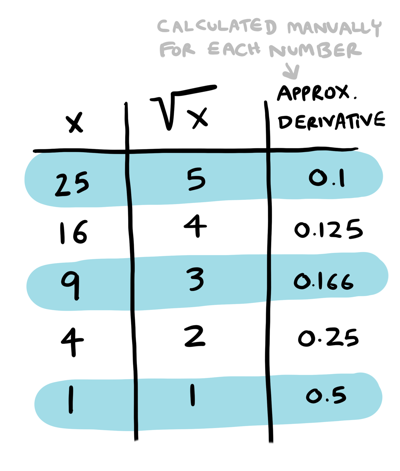
I have calculated some values for the derivative manually, but it is a little tougher to figure out what the derivative function is here (spoiler: it is \(1/(2 * sqrt(x)\)).
In the next section, I will show how to calculate the derivative function, so you can easily calculate the derivative at any point without having to go through the output change / input change calculation every time.
P.S. While we are here, why not use this table to estimate the square root of \(26\)? I bet this would have been really hard to do without derivatives, but with derivatives it is easy:
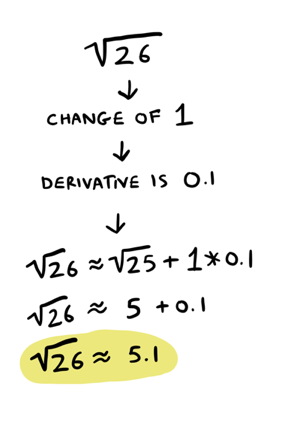
So the square root of \(26\) is approximately \(5.1\). Here's a more exact result from WolframAlpha. We were very close!
How To Calculate The Derivative
Calculating the derivative isn't too different from what we did when we plugged in numbers. We used output change / input change to calculate the derivative at \(4\):
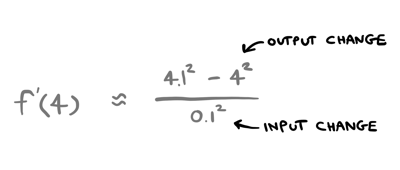
I could write the ratio slightly differently like this:
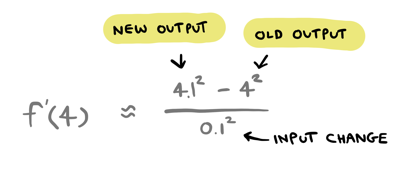
This isn't too different, we can figure out that the output change is the difference between the old and new input.
Now this time, instead of plugging in numbers, we will plug in variables and do some algebra! Suppose the input change we are making is \(c\). What is the old output? What is the new output?
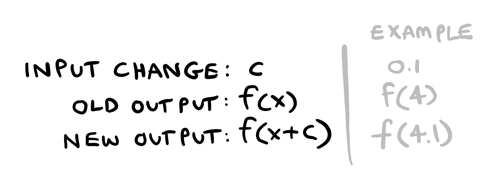
Putting it all together:
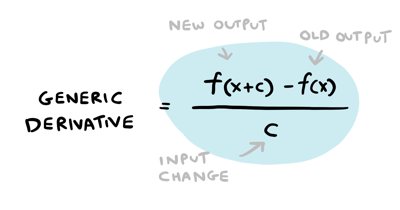
The formula is the same, we're just using variables instead of numbers. Now we know that \(f(x) = x^2\), which means \(f(x + c) = (x + c)^2\). Lets make that substitution:
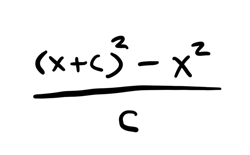
Now we can expand:
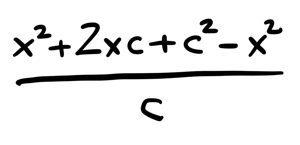
And simplify:
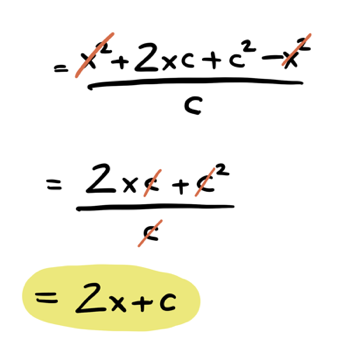
And we're left with:
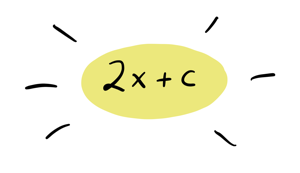
Which looks a LOT like what we KNOW is the derivative: \(2x\)!
By doing the same output change / input change but with variables instead of numbers, we seem to have gotten close to figuring out the derivative function, not just calculating the derivative at a particular point!
We are almost there, there's one last wrinkle to talk about: limits.
Limits
Remember when we were calculating the derivative at \(4\)? I had told you the derivative at 4 is 8. When we calculated it manually, it seemed like as we made the input change smaller, the value got closer and closer to \(8\):
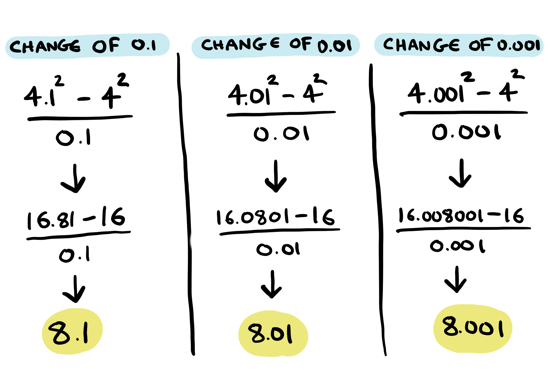
It seems like the value would be \(8\) if we could just make the input change small enough! This is an important part of figuring out the derivative: you need to ask yourself "what is the value approaching when I make the change smaller?"
Lets look again at what we calculated using algebra. What happens if you keep making the input change smaller?
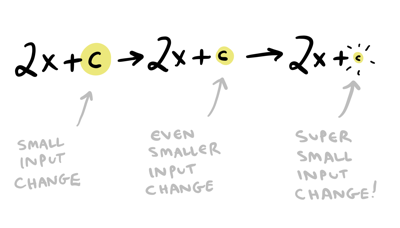
Hey, the \(c\) just keeps getting smaller and smaller! We can also see this if we plug in the numbers into \(2x + c\):
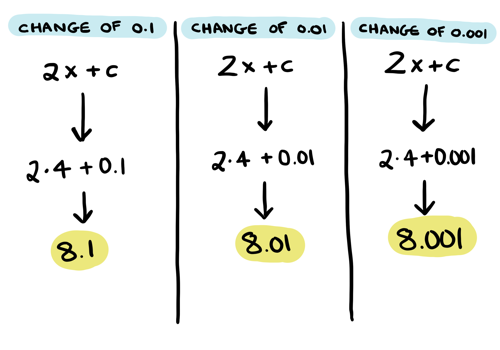
The output looks a lot like our manual calculations! That change \(c\) never truly goes away, but it is so small that it doesn't really matter: if you make \(c\) small enough, the derivative is basically \(8\). So we're just going to pretend that all the \(c\)s are so small they have become zero. Which leaves us with this as the derivative:
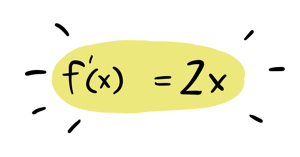
Do you feel a little dissatisfied? It doesn't feel very precise, does it? When we started out estimating \(7.1^2\), that's why it was an estimate. Derivatives won't give you an exact answer, just an estimate. The good news is, you can get an estimate that is as precise as you like. We used the derivative at \(7\) to estimate \(7.1\), which gave us a pretty good estimate. We could have used the derivative at \(4\) instead, to get a worse estimate:
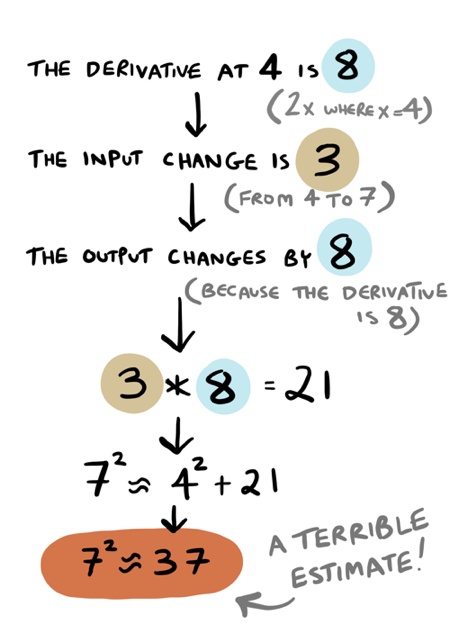
Remember, the smaller the change, the more precise the result. Since \(4 -> 7.1\) is a bigger change than \(7 -> 7.1\), the result is less precise.
That's all I will say about limits, but you can learn more by taking this excellent Calculus course by Jim Fowler!
Now we're ready for the official definition of derivative:
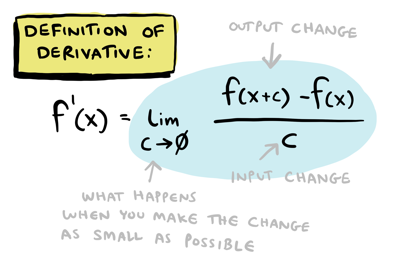
As I said earlier, the derivative is the output change over the input change! That \(lim\) bit is read as "the limit as \(c\) goes to zero" and is the mathematical way of writing exactly what we just discussed: what's the derivative if you make the change small enough?
You can calculate any derivative using this definition, just like we did for \(f(x) = x^2\). But there are also shortcuts for calculating the derivative! I'll get to those later on in the post.
Interlude: How To Visualize The Derivative
I think this is a neat way to visualize the derivative.
Here's one way to visualize \(f(x) = x^2\): picture a square with sides length \(x\). It's area is then \(x^2\):
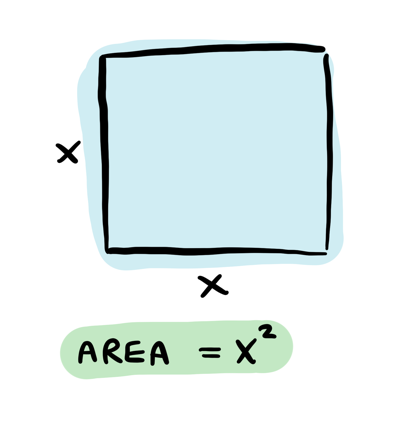
If I increase the length of a side, how does the area change? For example, if I go from sides length \(4\) to \(4.1\):
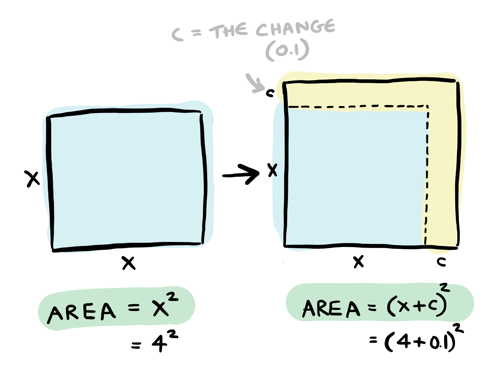
How does the area change? \(c\) represents the change, which is 0.1 in this case. We took the old square and added on some pieces:
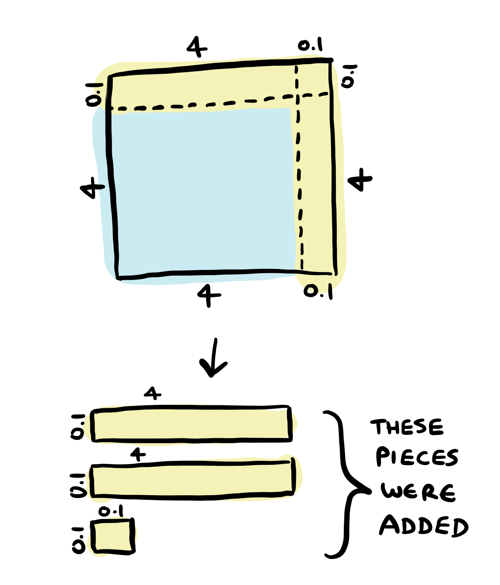
Those yellow pieces are the output change. You can see there are two rectangles of area \(c * x\), and one square of area \(c^2\). So the additional area is \(2cx + c^2\).
Now remember that the derivative is actually the ratio of output change to input change:

Which in this case would be:
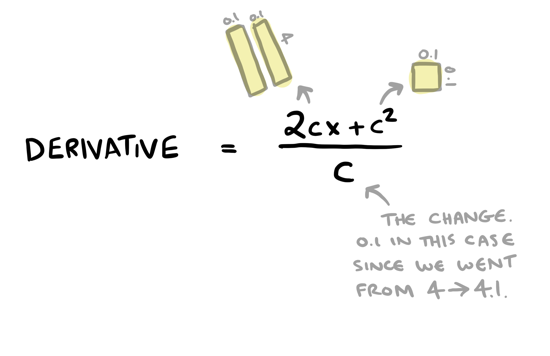
You can simplify this fraction:
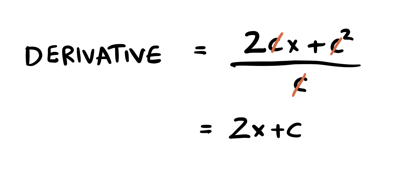
And based on our conversation about limits, we can throw away the \(c\). So the derivative is \(2x\)!
FAQ
As we moved from 4 to 5, the derivative changed from 8 to 10. What does that mean?
Suppose we have two squares, one with side length \(4\) and the other with side length \(10\):
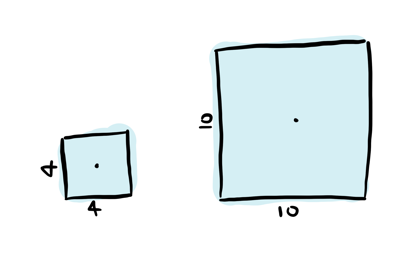
Now suppose you increase the side length by \(0.1\) for both boxes:
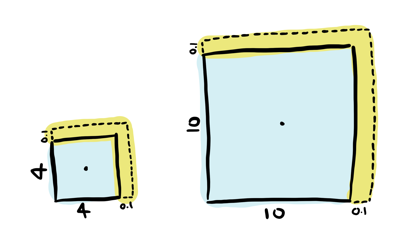
Notice that the total area increased by MORE for the \(10\) box than the \(4\) box:
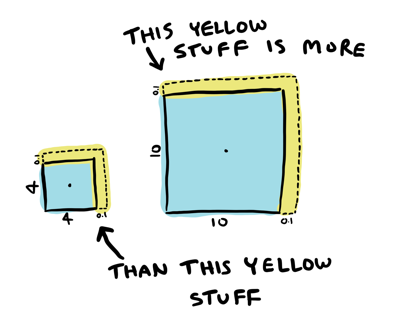
I increased the length of the box side by the same amount. But the area grew by different amounts:
The area of the size \(10\) box increased by more than the area of the size \(4\) box.
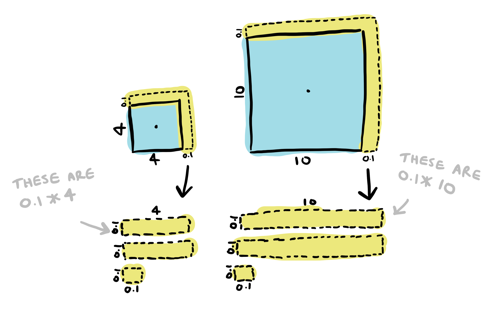
For bigger boxes, the input change leads to a bigger output change. Back to the table:

The output changes by a factor of \(8\) if the box is a size \(4\), but it changes by a factor of \(14\) if the box is a size \(7\). For a box of size \(10\), the output changes by a factor of \(20\).
When we estimated 5.1^2, why did we use the derivative at 5 instead of the derivative at 4?
Suppose I want to use \(4^2\) to calculate \(5^2\).
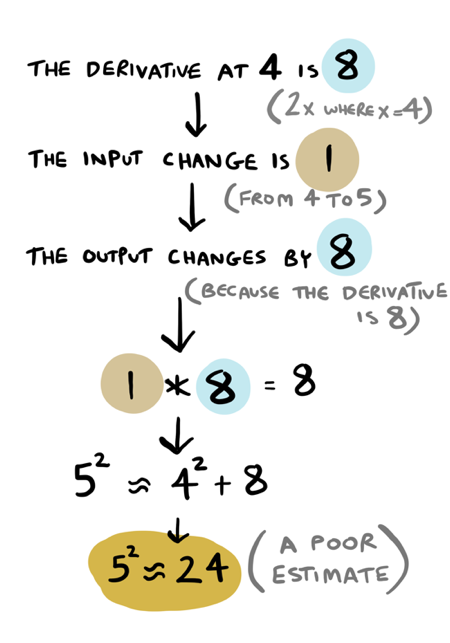
That is off by one, not great.
Or suppose I want to use \(4^2\) to calculate \(100^2\).

\(100^2\) is actually \(10000\), so that is off by a LOT! That makes sense, because although \(f'(4) = 8\), \(f'(100) = 200\). The ratios are wildly different so the estimate is not as good. The closer your derivative is to the number, the better your estimate will be.
What if we used \(200\) as the ratio instead? \(4^2 + (96*200) = 16 + 19200 = 19216\). So we know the answer is somewhere between \(784\) and \(19216\).
Remember: The smaller the change, the more accurate your estimate will be.
Power rule, chain rule
At this point you know what the derivative is, and how to find it. But calculating the derivative using the definition can get tedious! I'll end the post by showing some shortcuts for finding the derivative.
Power rule
The power rule is a simple way to calculate derivatives:
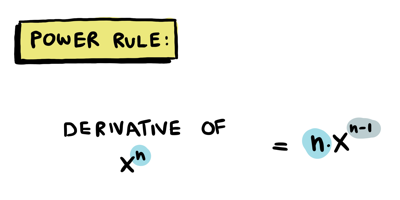
Some examples:
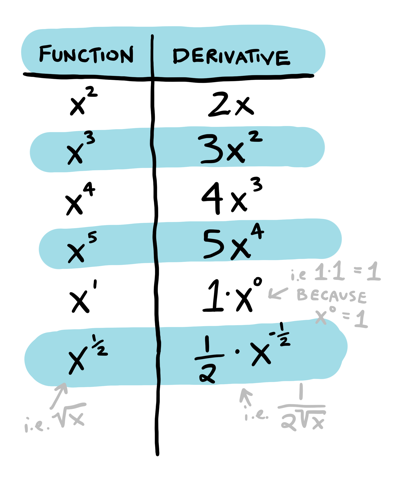
You can see the derivative of \(x^2\) is \(2x\), as we knew it would be. The other derivatives are interesting and would have taken more work to calculate without the power rule!
The power rule also works when there are multiple terms being added or subtracted:
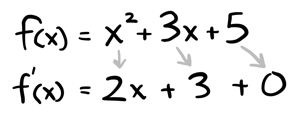
Another example:
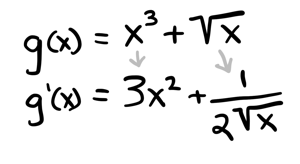
In general, if you have multiple terms being added or subtracted, you can apply all the rules here (power rule, product rule etc) to individual terms. To quote Jim Fowler's excellent Coursera course:
The derivative of a sum is the sum of the derivatives.
You can also always calculate these using the definition of the derivative, though that takes more work. Here's an example:
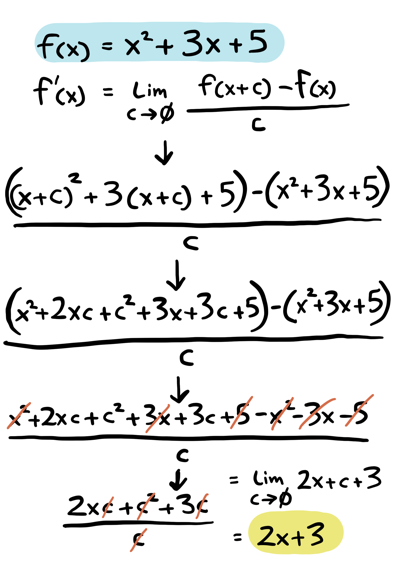
Product rule
How would you find the derivative of something like this?
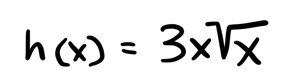
Use the product rule:
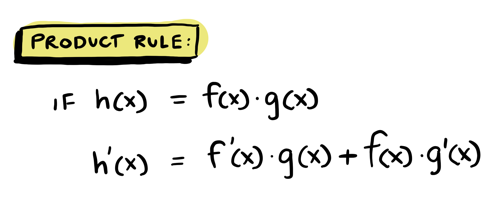
Example:
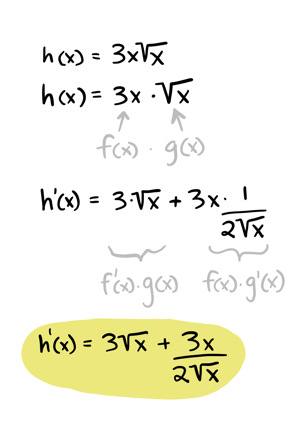
Here's how you could find the derivative of \(x^2\) using the product rule:
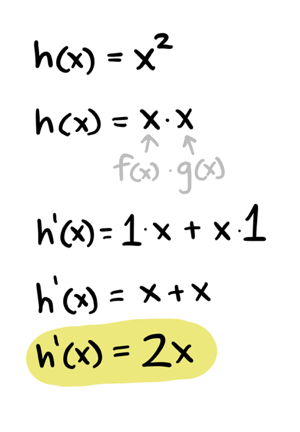
Quotient rule
What if something is being divided? Use the quotient rule:
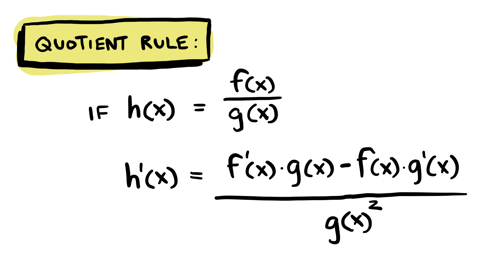
Example:
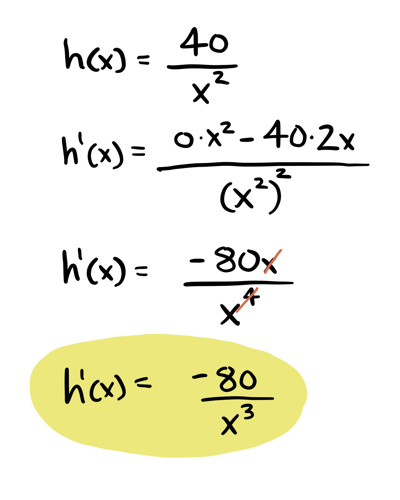
Chain rule
What if you have two functions that are nested? Use the chain rule!
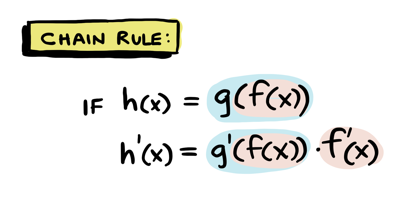
This is really handy when you come across something complicated like this:
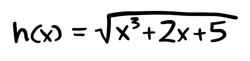
This is a complicated thing to differentiate, but we can break it apart into two functions!
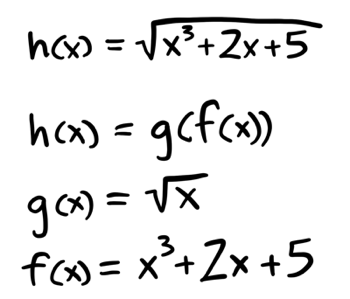
One function is just the square root, the other function is that complicated thing inside.
You can find the derivatives of those two functions separately:
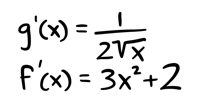
Then use the chain rule. To calculate \(g'(f(x))\), we take the derivative of \(g(x)\), and everywhere you see \(x\), substitute \(f(x)\) (i.e. \(x^3 + 2x + 5\)).
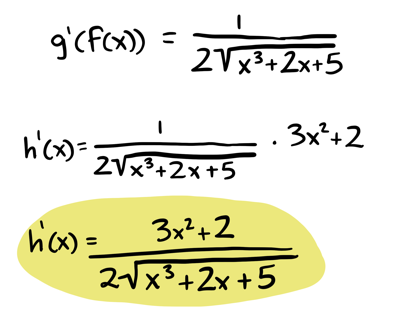
Finally, if you need help you can always ask WolframAlpha to find the derivative for you. Here's an example and a more complicated example.
Recap
- The derivative tells you the ratio of output change to input change.
- Given an input change, you can use the derivative to estimate what the output change will be.
- You can calculate the derivative yourself using the definition of the derivative.
- To calculate the derivative, you have to see what it is converging to as you make the change smaller aond smaller.
- The derivative is potentially changing at every point!
Remember this important takeaway:

You can always use the definition to calculate the derivative:

This was a quick introduction to derivatives. 3Blue1Brown also has good videos for building intuition on calculus. But maybe you are like me and want a complete, well-thought out course to study from, with practice questions, so you can say you truly understand calculus. If so, I cannot recommend Jim Fowler's Coursera course highly enough. He is a terrific teacher.
Finally, if you want to read more illustrated math blog posts, check out my post on linear regression.